hump.vector¶

vector = require "hump.vector"

A handy 2D vector class providing most of the things you do with vectors.

You can access the individual coordinates by vec.x and vec.y.

Note

The vectors are stored as tables. Most operations create new vectors and thus new tables, which may put the garbage collector under stress. If you experience slowdowns that are caused by hump.vector, try the table-less version hump.vector-light.

Example:

function player:update(dt)
    local delta = vector(0,0)
    if love.keyboard.isDown('left') then
        delta.x = -1
    elseif love.keyboard.isDown('right') then
        delta.x =  1
    end
    if love.keyboard.isDown('up') then
        delta.y = -1
    elseif love.keyboard.isDown('down') then
        delta.y =  1
    end
    delta:normalizeInplace()

    player.velocity = player.velocity + delta * player.acceleration * dt

    if player.velocity:len() > player.max_velocity then
        player.velocity = player.velocity:normalized() * player.max_velocity
    end

    player.position = player.position + player.velocity * dt
end

Vector arithmetic¶

hump provides vector arithmetic by implement the corresponding metamethods (__add, __mul, etc.). Here are the semantics:

vector + vector = vector: Component wise sum: \((a,b) + (x,y) = (a+x, b+y)\)
vector - vector = vector: Component wise difference: \((a,b) - (x,y) = (a-x, b-y)\)
vector * vector = number: Dot product: \((a,b) \cdot (x,y) = a\cdot x + b\cdot y\)
number * vector = vector: Scalar multiplication/scaling: \((a,b) \cdot s = (s\cdot a, s\cdot b)\)
vector * number = vector: Scalar multiplication/scaling: \(s \cdot (x,y) = (s\cdot x, s\cdot y)\)
vector / number = vector: Scalar division: \((a,b) / s = (a/s, b/s)\).
vector // number = vector: Scalar integer division (only Lua 5.3 and up): \((a,b) // s = (a//s, b//s)\).

Common relations are also defined:

a == b: Same as a.x == b.x and a.y == b.y.
a <= b: Same as a.x <= b.x and a.y <= b.y.
a < b: Lexicographical order: a.x < b.x or (a.x == b.x and a.y < b.y).

Example:

-- acceleration, player.velocity and player.position are vectors
acceleration = vector(0,-9)
player.velocity = player.velocity + acceleration * dt
player.position = player.position + player.velocity * dt

Function Reference¶

vector.new(x, y)¶

Arguments:	x,y (numbers) – Coordinates.
Returns:	The vector.

Create a new vector.

Examples:

a = vector.new(10,10)

-- as a shortcut, you can call the module like a function:
vector = require "hump.vector"
a = vector(10,10)

vector.fromPolar(angle, radius)¶

Arguments:	angle (number) – Angle of the vector in radians. radius (number) – Length of the vector (optional, default = 1).
Returns:	The vector in cartesian coordinates.

Create a new vector from polar coordinates. The angle is measured against the vector (1,0), i.e., the x axis.

Examples:

a = vector.polar(math.pi,10)

vector.randomDirection(len_min, len_max)¶

Arguments:	len_min (number) – Minimum length of the vector (optional, default = 1). len_max (number) – Maximum length of the vector (optional, default = `len_min`).
Returns:	A vector pointing in a random direction with a random length between `len_min` and `len_max`.

Examples:

rnd = vector.randomDirection()    -- length is 1
rnd = vector.randomDirection(100) -- length is 100
rnd = vector.randomDirection(1,5) -- length is a random value between 1 and 5

Sample a vector with random direction and (optional) length.

vector.isvector(v)¶

Arguments:	v (mixed) – The variable to test.
Returns:	`true` if `v` is a vector, `false` otherwise.

Test whether a variable is a vector.

Example:

if not vector.isvector(v) then
    v = vector(v,0)
end

vector:clone()¶

Returns:	Copy of the vector.

Copy a vector. Assigning a vector to a variable will create a reference, so when modifying the vector referenced by the new variable would also change the old one:

a = vector(1,1) -- create vector
b = a           -- b references a
c = a:clone()   -- c is a copy of a
b.x = 0         -- changes a,b and c
print(a,b,c)    -- prints '(1,0), (1,0), (1,1)'

Example:

copy = original:clone()

vector:unpack()¶

Returns:	The coordinates `x,y`.

Extract coordinates.

Examples:

x,y = pos:unpack()

love.graphics.draw(self.image, self.pos:unpack())

vector:permul(other)¶

Arguments:	other (vector) – The second source vector.
Returns:	Vector whose components are products of the source vectors.

Multiplies vectors coordinate wise, i.e. result = vector(a.x * b.x, a.y * b.y).

Does not change either argument vectors, but creates a new one.

Example:

-- scale with different magnitudes
scaled = original:permul(vector(1,1.5))

vector:len()¶

Returns:	Length of the vector.

Get length of the vector, i.e. math.sqrt(vec.x * vec.x + vec.y * vec.y).

Example:

distance = (a - b):len()

vector:toPolar()¶

Returns:	The vector in polar coordinates (angle, radius).

Convert the vector to polar coordinates, i.e., the angle and the radius/lenth.

Example:

-- complex multiplication
p, q = a:toPolar(), b:toPolar()
c = vector(p.x+q.x, p.y*q.y)

vector:len2()¶

Returns:	Squared length of the vector.

Get squared length of the vector, i.e. vec.x * vec.x + vec.y * vec.y.

Example:

-- get closest vertex to a given vector
closest, dsq = vertices[1], (pos - vertices[1]):len2()
for i = 2,#vertices do
    local temp = (pos - vertices[i]):len2()
    if temp < dsq then
        closest, dsq = vertices[i], temp
    end
end

vector:dist(other)¶

Arguments:	other (vector) – Other vector to measure the distance to.
Returns:	The distance of the vectors.

Get distance of two vectors. The same as (a - b):len().

Example:

-- get closest vertex to a given vector
-- slightly slower than the example using len2()
closest, dist = vertices[1], pos:dist(vertices[1])
for i = 2,#vertices do
    local temp = pos:dist(vertices[i])
    if temp < dist then
        closest, dist = vertices[i], temp
    end
end

vector:dist2(other)¶

Arguments:	other (vector) – Other vector to measure the distance to.
Returns:	The squared distance of the vectors.

Get squared distance of two vectors. The same as (a - b):len2().

Example:

-- get closest vertex to a given vector
-- slightly faster than the example using len2()
closest, dsq = vertices[1], pos:dist2(vertices[1])
for i = 2,#vertices do
    local temp = pos:dist2(vertices[i])
    if temp < dsq then
        closest, dsq = vertices[i], temp
    end
end

vector:normalized()¶

Returns:	Vector with same direction as the input vector, but length 1.

Get normalized vector: a vector with the same direction as the input vector, but with length 1.

Does not change the input vector, but creates a new vector.

Example:

direction = velocity:normalized()

vector:normalizeInplace()¶

Returns:	Itself – the normalized vector

Normalize a vector, i.e. make the vector to have length 1. Great to use on intermediate results.

Warning

This modifies the vector. If in doubt, use vector:normalized().

Example:

normal = (b - a):perpendicular():normalizeInplace()

vector:rotated(angle)¶

Arguments:	angle (number) – Rotation angle in radians.
Returns:	The rotated vector

Get a vector with same length, but rotated by angle:

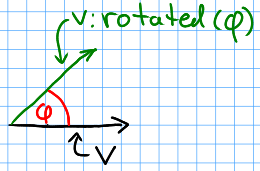
Does not change the input vector, but creates a new vector.

Example:

-- approximate a circle
circle = {}
for i = 1,30 do
    local phi = 2 * math.pi * i / 30
    circle[#circle+1] = vector(0,1):rotated(phi)
end

vector:rotateInplace(angle)¶

Arguments:	angle (number) – Rotation angle in radians.
Returns:	Itself – the rotated vector

Rotate a vector in-place. Great to use on intermediate results.

Warning

This modifies the vector. If in doubt, use vector:rotated().

Example:

-- ongoing rotation
spawner.direction:rotateInplace(dt)

vector:perpendicular()¶

Returns:	A vector perpendicular to the input vector

Quick rotation by 90°. Creates a new vector. The same (but faster) as vec:rotate(math.pi/2):

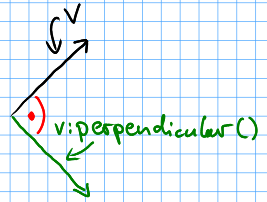
Example:

normal = (b - a):perpendicular():normalizeInplace()

vector:projectOn(v)¶

Arguments:	v (vector) – The vector to project on.
Returns:	`vector` The projected vector.

Project vector onto another vector:

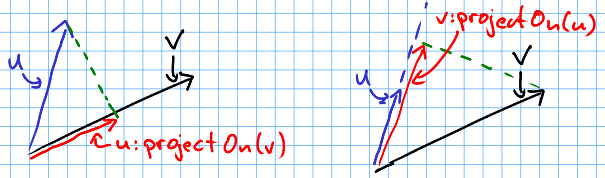
Example:

velocity_component = velocity:projectOn(axis)

vector:mirrorOn(v)¶

Arguments:	v (vector) – The vector to mirror on.
Returns:	The mirrored vector.

Mirrors vector on the axis defined by the other vector:

Example:

deflected_velocity = ball.velocity:mirrorOn(surface_normal)

vector:cross(other)¶

Arguments:	other (vector) – Vector to compute the cross product with.
Returns:	`number` Cross product of both vectors.

Get cross product of two vectors. Equals the area of the parallelogram spanned by both vectors.

Example:

parallelogram_area = a:cross(b)

vector:angleTo(other)¶

Arguments:	other (vector) – Vector to measure the angle to (optional).
Returns:	Angle in radians.

Measures the angle between two vectors. If other is omitted it defaults to the vector (0,0), i.e. the function returns the angle to the coordinate system.

Example:

lean = self.upvector:angleTo(vector(0,1))
if lean > .1 then self:fallOver() end

vector:trimmed(max_length)¶

Arguments:	max_length (number) – Maximum allowed length of the vector.
Returns:	A trimmed vector.

Trim the vector to max_length, i.e. return a vector that points in the same direction as the source vector, but has a magnitude smaller or equal to max_length.

Does not change the input vector, but creates a new vector.

Example:

ship.velocity = ship.force * ship.mass * dt
ship.velocity = ship.velocity:trimmed(299792458)

vector:trimInplace(max_length)¶

Arguments:	max_length (number) – Maximum allowed length of the vector.
Returns:	Itself – the trimmed vector.

Trim the vector to max_length, i.e. return a vector that points in the same direction as the source vector, but has a magnitude smaller or equal to max_length.

Warning

This modifies the vector. If in doubt, use vector:trimmed().

Example:

ship.velocity = (ship.velocity + ship.force * ship.mass * dt):trimInplace(299792458)

hump.vector¶

List of Functions¶

Vector arithmetic¶

Function Reference¶